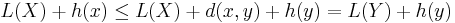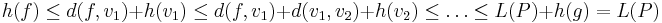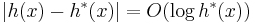A* search algorithm
In computer science, A* (pronounced "A star" ( listen)) is a computer algorithm that is widely used in pathfinding and graph traversal, the process of plotting an efficiently traversable path between points, called nodes. Noted for its performance and accuracy, it enjoys widespread use. Peter Hart, Nils Nilsson and Bertram Raphael first described the algorithm in 1968.[1] It is an extension of Edsger Dijkstra's 1959 algorithm. A* achieves better performance (with respect to time) by using heuristics.
Contents |
Description
A* uses a best-first search and finds a least-cost path from a given initial node to one goal node (out of one or more possible goals).
It uses a distance-plus-cost heuristic function (usually denoted  ) to determine the order in which the search visits nodes in the tree. The distance-plus-cost heuristic is a sum of two functions:
) to determine the order in which the search visits nodes in the tree. The distance-plus-cost heuristic is a sum of two functions:
- the path-cost function, which is the cost from the starting node to the current node (usually denoted
 )
) - and an admissible "heuristic estimate" of the distance to the goal (usually denoted
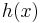 ).
).
The 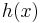 part of the
part of the  function must be an admissible heuristic; that is, it must not overestimate the distance to the goal. Thus, for an application like routing,
function must be an admissible heuristic; that is, it must not overestimate the distance to the goal. Thus, for an application like routing, 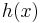 might represent the straight-line distance to the goal, since that is physically the smallest possible distance between any two points or nodes.
might represent the straight-line distance to the goal, since that is physically the smallest possible distance between any two points or nodes.
If the heuristic h satisfies the additional condition 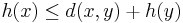 for every edge x, y of the graph (where d denotes the length of that edge), then h is called monotone, or consistent. In such a case, A* can be implemented more efficiently—roughly speaking, no node needs to be processed more than once (see closed set below)—and A* is equivalent to running Dijkstra's algorithm with the reduced cost
for every edge x, y of the graph (where d denotes the length of that edge), then h is called monotone, or consistent. In such a case, A* can be implemented more efficiently—roughly speaking, no node needs to be processed more than once (see closed set below)—and A* is equivalent to running Dijkstra's algorithm with the reduced cost 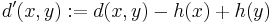 .
.
Note that A* has been generalized into a bidirectional heuristic search algorithm; see bidirectional search.
History
In 1964 Nils Nilsson invented a heuristic based approach to increase the speed of Dijkstra's algorithm. This algorithm was called A1. In 1967 Bertram Raphael made dramatic improvements upon this algorithm, but failed to show optimality. He called this algorithm A2. Then in 1968 Peter E. Hart introduced an argument that proved A2 was optimal when using a consistent heuristic with only minor changes. His proof of the algorithm also included a section that showed that the new A2 algorithm was the best algorithm possible given the conditions. He thus named the new algorithm in Kleene star syntax to be the algorithm that starts with A and includes all possible version numbers or A*. [2]
Concepts
As A* traverses the graph, it follows a path of the lowest known cost, keeping a sorted priority queue of alternate path segments along the way. If, at any point, a segment of the path being traversed has a higher cost than another encountered path segment, it abandons the higher-cost path segment and traverses the lower-cost path segment instead. This process continues until the goal is reached.
Process
Like all informed search algorithms, it first searches the routes that appear to be most likely to lead towards the goal. What sets A* apart from a greedy best-first search is that it also takes the distance already traveled into account; the 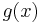 part of the heuristic is the cost from the starting point, not simply the local cost from the previously expanded node.
part of the heuristic is the cost from the starting point, not simply the local cost from the previously expanded node.
Starting with the initial node, it maintains a priority queue of nodes to be traversed, known as the open set. The lower  for a given node
for a given node  , the higher its priority. At each step of the algorithm, the node with the lowest
, the higher its priority. At each step of the algorithm, the node with the lowest  value is removed from the queue, the
value is removed from the queue, the  and
and  values of its neighbors are updated accordingly, and these neighbors are added to the queue. The algorithm continues until a goal node has a lower
values of its neighbors are updated accordingly, and these neighbors are added to the queue. The algorithm continues until a goal node has a lower  value than any node in the queue (or until the queue is empty). (Goal nodes may be passed over multiple times if there remain other nodes with lower
value than any node in the queue (or until the queue is empty). (Goal nodes may be passed over multiple times if there remain other nodes with lower  values, as they may lead to a shorter path to a goal.) The
values, as they may lead to a shorter path to a goal.) The  value of the goal is then the length of the shortest path, since
value of the goal is then the length of the shortest path, since  at the goal is zero in an admissible heuristic. If the actual shortest path is desired, the algorithm may also update each neighbor with its immediate predecessor in the best path found so far; this information can then be used to reconstruct the path by working backwards from the goal node. Additionally, if the heuristic is monotonic (or consistent, see below), a closed set of nodes already traversed may be used to make the search more efficient.
at the goal is zero in an admissible heuristic. If the actual shortest path is desired, the algorithm may also update each neighbor with its immediate predecessor in the best path found so far; this information can then be used to reconstruct the path by working backwards from the goal node. Additionally, if the heuristic is monotonic (or consistent, see below), a closed set of nodes already traversed may be used to make the search more efficient.
Pseudocode
The following pseudocode describes the algorithm:
function A*(start,goal) closedset := the empty set // The set of nodes already evaluated. openset := {start} // The set of tentative nodes to be evaluated, initially containing the start node came_from := the empty map // The map of navigated nodes. g_score[start] := 0 // Cost from start along best known path. h_score[start] := heuristic_cost_estimate(start, goal) f_score[start] := g_score[start] + h_score[start] // Estimated total cost from start to goal through y. while openset is not empty x := the node in openset having the lowest f_score[] value if x = goal return reconstruct_path(came_from, came_from[goal]) remove x from openset add x to closedset foreach y in neighbor_nodes(x) if y in closedset continue tentative_g_score := g_score[x] + dist_between(x,y) if y not in openset add y to openset tentative_is_better := true else if tentative_g_score < g_score[y] tentative_is_better := true else tentative_is_better := false if tentative_is_better = true came_from[y] := x g_score[y] := tentative_g_score h_score[y] := heuristic_cost_estimate(y, goal) f_score[y] := g_score[y] + h_score[y] return failure function reconstruct_path(came_from, current_node) if came_from[current_node] is set p := reconstruct_path(came_from, came_from[current_node]) return (p + current_node) else return current_node
Remark: the above pseudocode assumes that the heuristic function is monotonic (or consistent, see below), which is a frequent case in many practical problems, such as the Shortest Distance Path in road networks. However, if the assumption is not true, nodes in the closed set may be rediscovered and their cost improved. In other words, the closed set can be omitted (yielding a tree search algorithm) if a solution is guaranteed to exist, or if the algorithm is adapted so that new nodes are added to the open set only if they have a lower  value than at any previous iteration.
value than at any previous iteration.
Example
An example of an A star (A*) algorithm in action where nodes are cities connected with roads and h(x) is the straight-line distance to target point:
Key: green: start; blue: goal; orange: visited
Note: This example uses a comma as the decimal separator.
Properties
Like breadth-first search, A* is complete and will always find a solution if one exists.
If the heuristic function  is admissible, meaning that it never overestimates the actual minimal cost of reaching the goal, then A* is itself admissible (or optimal) if we do not use a closed set. If a closed set is used, then
is admissible, meaning that it never overestimates the actual minimal cost of reaching the goal, then A* is itself admissible (or optimal) if we do not use a closed set. If a closed set is used, then  must also be monotonic (or consistent) for A* to be optimal. This means that for any pair of adjacent nodes
must also be monotonic (or consistent) for A* to be optimal. This means that for any pair of adjacent nodes  and
and  , where
, where 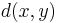 denotes the length of the edge between them, we must have:
denotes the length of the edge between them, we must have:
This ensures that for any path  from the initial node to
from the initial node to  :
:
where 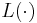 denotes the length of a path, and
denotes the length of a path, and  is the path
is the path  extended to include
extended to include  . In other words, it is impossible to decrease (total distance so far + estimated remaining distance) by extending a path to include a neighboring node. (This is analogous to the restriction to nonnegative edge weights in Dijkstra's algorithm.) Monotonicity implies admissibility when the heuristic estimate at any goal node itself is zero, since (letting
. In other words, it is impossible to decrease (total distance so far + estimated remaining distance) by extending a path to include a neighboring node. (This is analogous to the restriction to nonnegative edge weights in Dijkstra's algorithm.) Monotonicity implies admissibility when the heuristic estimate at any goal node itself is zero, since (letting 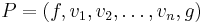 be a shortest path from any node
be a shortest path from any node  to the nearest goal
to the nearest goal  ):
):
A* is also optimally efficient for any heuristic  , meaning that no algorithm employing the same heuristic will expand fewer nodes than A*, except when there are multiple partial solutions where
, meaning that no algorithm employing the same heuristic will expand fewer nodes than A*, except when there are multiple partial solutions where  exactly predicts the cost of the optimal path. Even in this case, for each graph there exists some order of breaking ties in the priority queue such that A* examines the fewest possible nodes.
exactly predicts the cost of the optimal path. Even in this case, for each graph there exists some order of breaking ties in the priority queue such that A* examines the fewest possible nodes.
Special cases
Dijkstra's algorithm, as another example of a uniform-cost search algorithm, can be viewed as a special case of A* where  for all
for all  . General depth-first search can be implemented using the A* by considering that there is a global counter C initialized with a very large value. Every time we process a node we assign C to all of its newly discovered neighbors. After each single assignment, we decrease the counter C by one. Thus the earlier a node is discovered, the higher its
. General depth-first search can be implemented using the A* by considering that there is a global counter C initialized with a very large value. Every time we process a node we assign C to all of its newly discovered neighbors. After each single assignment, we decrease the counter C by one. Thus the earlier a node is discovered, the higher its 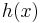 value. It should be noted, however, that both Dijkstra's algorithm and depth-first search can be implemented more efficiently without including a
value. It should be noted, however, that both Dijkstra's algorithm and depth-first search can be implemented more efficiently without including a 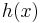 value at each node.
value at each node.
Implementation details
There are a number of simple optimizations or implementation details that can significantly affect the performance of an A* implementation. The first detail to note is that the way the priority queue handles ties can have a significant effect on performance in some situations. If ties are broken so the queue behaves in a LIFO manner, A* will behave like depth-first search among equal cost paths.
When a path is required at the end of the search, it is common to keep with each node a reference to that node's parent. At the end of the search these references can be used to recover the optimal path. If these references are being kept then it can be important that the same node doesn't appear in the priority queue more than once (each entry corresponding to a different path to the node, and each with a different cost). A standard approach here is to check if a node about to be added already appears in the priority queue. If it does, then the priority and parent pointers are changed to correspond to the lower cost path. When finding a node in a queue to perform this check, many standard implementations of a min-heap require 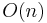 time. Augmenting the heap with a hash table can reduce this to constant time.
time. Augmenting the heap with a hash table can reduce this to constant time.
Admissibility and optimality
A* is admissible and considers fewer nodes than any other admissible search algorithm with the same heuristic. This is because A* uses an "optimistic" estimate of the cost of a path through every node that it considers—optimistic in that the true cost of a path through that node to the goal will be at least as great as the estimate. But, critically, as far as A* "knows", that optimistic estimate might be achievable.
Here is the main idea of the proof:
When A* terminates its search, it has found a path whose actual cost is lower than the estimated cost of any path through any open node. But since those estimates are optimistic, A* can safely ignore those nodes. In other words, A* will never overlook the possibility of a lower-cost path and so is admissible.
Suppose now that some other search algorithm B terminates its search with a path whose actual cost is not less than the estimated cost of a path through some open node. Based on the heuristic information it has, Algorithm B cannot rule out the possibility that a path through that node has a lower cost. So while B might consider fewer nodes than A*, it cannot be admissible. Accordingly, A* considers the fewest nodes of any admissible search algorithm.
This is only true if both:
- A* uses an admissible heuristic. Otherwise, A* is not guaranteed to expand fewer nodes than another search algorithm with the same heuristic. See (Generalized best-first search strategies and the optimality of A*, Rina Dechter and Judea Pearl, 1985[3])
- A* solves only one search problem rather than a series of similar search problems. Otherwise, A* is not guaranteed to expand fewer nodes than incremental heuristic search algorithms. See (Incremental heuristic search in artificial intelligence, Sven Koenig, Maxim Likhachev, Yaxin Liu and David Furcy, 2004[4])
Weighted A*
Weighted A* is a variant of the A* algorithm that lets one speed-up a search at the expense of optimality. The basic idea is to "inflate" an admissible heuristic to speed up the search, and yet have a bound on the sub-optimality. If 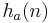 is an admissible heuristic function, in the weighted version of the A* search one uses
is an admissible heuristic function, in the weighted version of the A* search one uses 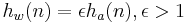 as the heuristic function, and perform the A* search as usual (which eventually happens faster than using
as the heuristic function, and perform the A* search as usual (which eventually happens faster than using 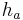 since fewer nodes are expanded). The path hence found by the search algorithm can have a cost of at most
since fewer nodes are expanded). The path hence found by the search algorithm can have a cost of at most 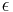 times that of the least cost path in the graph.[5]
times that of the least cost path in the graph.[5]
Complexity
The time complexity of A* depends on the heuristic. In the worst case, the number of nodes expanded is exponential in the length of the solution (the shortest path), but it is polynomial when the search space is a tree, there is a single goal state, and the heuristic function h meets the following condition:
where 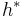 is the optimal heuristic, the exact cost to get from
is the optimal heuristic, the exact cost to get from  to the goal. In other words, the error of h will not grow faster than the logarithm of the “perfect heuristic”
to the goal. In other words, the error of h will not grow faster than the logarithm of the “perfect heuristic” 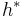 that returns the true distance from x to the goal (see Pearl 1984[6] and also Russell and Norvig 2003, p. 101[7])
that returns the true distance from x to the goal (see Pearl 1984[6] and also Russell and Norvig 2003, p. 101[7])
Variants of A*
- D*
- D* Lite
- Field D*
- IDA*
- Fringe
- Fringe Saving A* (FSA*)
- Generalized Adaptive A* (GAA*)
- Lifelong Planning A* (LPA*)
- SMA*
- Theta*
References
- Hart, P. E.; Nilsson, N. J.; Raphael, B. (1972). "Correction to "A Formal Basis for the Heuristic Determination of Minimum Cost Paths"". SIGART Newsletter 37: 28–29.
- Nilsson, N. J. (1980). Principles of Artificial Intelligence. Palo Alto, California: Tioga Publishing Company. ISBN 0-935382-01-1.
- Pearl, Judea (1984). Heuristics: Intelligent Search Strategies for Computer Problem Solving. Addison-Wesley. ISBN 0-201-05594-5.
- ^ Hart, P. E.; Nilsson, N. J.; Raphael, B. (1968). "A Formal Basis for the Heuristic Determination of Minimum Cost Paths". IEEE Transactions on Systems Science and Cybernetics SSC4 4 (2): 100–107. doi:10.1109/TSSC.1968.300136.
- ^ eecs.berkeley.edu
- ^ Dechter, Rina; Judea Pearl (1985). "Generalized best-first search strategies and the optimality of A*". Journal of the ACM 32 (3): 505–536. doi:10.1145/3828.3830. http://portal.acm.org/citation.cfm?id=3830&coll=portal&dl=ACM.
- ^ Koenig, Sven; Maxim Likhachev, Yaxin Liu, David Furcy (2004). "Incremental heuristic search in AI". AI Magazine 25 (2): 99–112. http://portal.acm.org/citation.cfm?id=1017140.
- ^ Pearl, Judea (1984). Heuristics: intelligent search strategies for computer problem solving. Addison-Wesley Longman Publishing Co., Inc.. ISBN 0-201-05594-5. http://portal.acm.org/citation.cfm?id=525.
- ^ Pearl, Judea (1984). Heuristics: Intelligent Search Strategies for Computer Problem Solving. Addison-Wesley. ISBN 0-201-05594-5.
- ^ Russell, S. J.; Norvig, P. (2003). Artificial Intelligence: A Modern Approach. Upper Saddle River, N.J.: Prentice Hall. pp. 97–104. ISBN 0-13-790395-2.
External links
- A* Pathfinding for Beginners
- A* with Jump point search
- Clear visual A* explanation, with advice and thoughts on path-finding
- Variation on A* called Hierarchical Path-Finding A* (HPA*)
- A* Algorithm tutorial